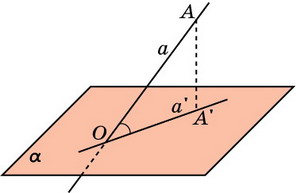
Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и её проекцией на данную плоскость.

• 0⁰<∠(a, α)<90⁰
  

• Угол между взаимно перпендикулярными прямой и плоскостью равен  90⁰
  
  

• Если прямая параллельна плоскости (или лежит в ней), то угол между ними считается равным  0⁰
  
  

Методы решения:   

• Классический метод: угол между прямой а и плоскостью α можно вычислить, используя различные факты из курса планиметрии касающиеся углав (теоремы синусов и косинусов, площадь треугольника, полная теорема синусов и др.).
• Векторно-координатный метод:
  угол между прямой а и плоскостью α можно вычислить по формуле:

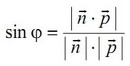
          или в координатной форме

                         ,  

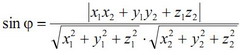         где 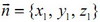 - вектор нормали плоскости  α,  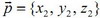 - направляющий вектор прямой а. 

         При этом следует заметить, что прямая а и плоскость α параллельны тогда и только тогда, когда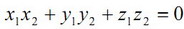   

Обучающая презентация* - скачать... 

Задачи для самостоятельного решения**

1.  В единичном кубе АС₁ найдите угол между прямой СD и плоскостью АВ₁D₁.

2. В единичном кубе АС₁ найдите угол между прямой А₁В₁ и плоскостью ВС₁D.

3. В единичном кубе АС₁ найдите угол между прямой АD₁ и плоскостью, проходящей через точки А₁, Е и F, где точка Е - середина ребра С₁D₁, точка F лежит на ребре DD₁, так, что D₁F=2DF.

4.  В единичном кубе АС₁ найдите угол между прямой АВ₁ и плоскостью АВС₁.

5.  В кубе АС₁ найдите угол между прямой А₁А и плоскостью ВС₁D.

6. В кубе АС₁ найдите угол между прямой АС₁ и плоскостью ВСС₁.

7. В кубе АС₁ точка Е - середина ребра А₁В₁. Найдите синус угла  между прямой АЕ и плоскостью ВD₁D.

8. В кубе АС₁ точка Е - середина ребра А₁В₁. Найдите синус угла  между прямой АЕ и плоскостью ВС₁D.

9. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁, АВ=2, АD=АА₁=1. Найдите угол между прямой АВ₁ и плоскостью АВС₁.

10. В прямоугольном параллелепипеде  ABCDA₁B₁C₁D₁ найдите угол между плоскостью АА₁С и прямой А₁В, если АА₁=3, АВ=4, ВС=4.

11. В прямоугольном параллелепипеде  ABCDA₁B₁C₁D₁ найдите угол между плоскостью ВА₁С и прямой С₁В, если АА₁=8, АВ=6, ВС=15.

12. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁, у которого  АА₁=4, А₁D₁=С₁D₁=6  найдите тангенс угла  между плоскостью АDD₁ и прямой EF, проходящей через середины рёбер АВ и В₁С₁.

13.  В прямоугольном параллелепипедеABCDA₁B₁C₁D₁, у которого  АВ=4, ВС=6, СС₁=4  найдите тангенс угла  между плоскостью АВС и прямой EF, проходящей через середины рёбер АА₁и D₁С₁.

14. В правильной треугольной призме АВСА₁В₁С₁, все рёбра которой равны 1, найдите угол между прямой АВ₁ и плоскостью АА₁С₁С.

15.  В правильной треугольной призме АВСА₁В₁С₁, все рёбра которой равны, найдите угол между прямой АА₁ и плоскостью АВС₁.

16.  В правильной треугольной призме АВСА₁В₁С₁, все рёбра которой равны 1, точка D - середина ребра А₁В₁. Найдите синус угла между прямой АD и плоскостью ВС₁С.

17. В основании прямой призмы МNКМ₁N₁К₁ лежит прямоугольный треугольник МNК, у которого угол N равен 90⁰, угол М равен 60⁰, NК=18. Диагональ боковой грани М₁N составляет угол 30⁰ с плоскостью ММ₁К₁. Найдите высоту призмы. 

18. В основании прямой призмы АВСА₁В₁С₁ лежит прямоугольный треугольник АВС, у которого угол С равен 90⁰, угол А равен 30⁰, АС=
10√3. Диагональ боковой грани В₁С составляет угол 30⁰ с плоскостью АА₁В₁. Найдите высоту призмы. 

19.  В правильной четырёхугольной призме  АВСDA₁B₁C₁D₁ сторона основания которой равна 5, а боковое ребро - 7, найдите угол между  прямой АВ₁ и плоскостью ВDD₁.

20. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁, все рёбра которой равны 1, найдите угол между прямой АВ₁ и плоскостью АСЕ₁.

21. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ сторона основания равна 3, а высота равна 1. Найдите угол между прямой F₁В₁ и плоскостью АF₁С₁.

22.  В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁, все рёбра которой равны 1, точка К - середина ребра А₁В₁. Найдите синус угла между прямой АК и плоскостью ВСС_1. 

23.  В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁, все рёбра которой равны 1, точка К - середина ребра С₁D₁. Найдите синус угла между прямой АК и плоскостью ВСС_1. 

24.  В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁, все рёбра которой равны 1, точка К - середина ребра А₁В₁. Найдите синус угла между прямой АК и плоскостью ВDD_1. 

25.  В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ сторона основания равна 7, а высота равна 1. Найдите угол между прямой F₁В₁ и плоскостью АF₁С₁.

26. В правильной треугольной пирамиде SАВС с основанием АВС известны рёбра: АВ=20√3, SС=29. Найдите угол, образованный плоскостью основания и прямой, проходящей через середины рёбер АS и ВС.

27. В правильной треугольной пирамиде МАВС с основанием АВС известны рёбра АВ=7√3, МС=25. Найти угол, образованный плоскостью основания и прямой, проходящей через середины рёбер АМ и ВС.

28.  В правильной треугольной пирамиде SАВС с основанием АВС известны рёбра: АВ=12√3, SС=13. Найдите угол, образованный плоскостью основания и прямой АМ, где точка М - точка пересечения медиан грани SВС. 

29.  В правильной треугольной пирамиде SАВС с основанием АВС сторона основания равна 2, а боковое ребро равно 3. Найдите угол между плоскостью ВSС и прямой МN, где точка N - середина ребра АС, а точка М лежит на ребре SВ так, что ВМ=1.

30. Дана правильная треугольная пирамида АВС, сторона основания и высота которой правны соответственно 6√3
и 4. Найдите угол между прямой ЕК и плоскостью основания АВС, если К - середина ребра DВ, а Е лежит на АD так, что АЕ:ЕD=3:1.

31.  В правильной треугольной пирамиде SАВС с основанием АВС сторона основания равна  
6√3, а боковое ребро равно 10. Найдите угол между плоскостью АВС и прямой МN, где точка N - середина ребра АС, а точка М лежит на ребре SВ так, что ВМ:МS=2:1. 

32. В правильной четырёхугольной пирамиде МАВСD, все рёбра которой равны 1, точка Е - середина ребра МС. Найдите синус угла между прямой DЕ и плоскостью АМВ.

33. В правильной четырёхугольной пирамиде SАВСD, все рёбра которой равны 1, точка Е - середина ребра МС. Найдите косинус угла между прямой АВ и плоскостью SAD.

34.  В правильной четырёхугольной пирамиде SАВСD,  которой АВ=3, SА=7, точка Е - середина ребра SВ. Найдите угол между прямой СЕ и плоскостою  SВD.
35.  В правильной четырёхугольной пирамиде МАВСD, все рёбра которой равны 1, точка Е - середина ребра МС. Найдите синус угла между прямой DЕ  и плоскостью АМВ.

35. В правильной четырёхугольной пирамиде МАВСD, все рёбра которой равны 1, найти угол между прямой DЕ, где Е - середина апофемы МF грани АМВ и плоскостью АМС.

36. В правильной шестиугольной пирамиде МАВСDЕF, стороны основания которой равны 1, а боковые рёбра равны 4, найти синус угла между прямой ВС и плоскостью ЕМD.

37.  В правильной шестиугольной пирамиде SАВСDЕF, стороны основания которой равны 1, а боковые рёбра равны 2, найти косинус угла между прямой АС и плоскостью SAF

* Презентация предоставлена  http://geometry2006.narod.ru/

** Задачи частично продоставлены http://alexlarin.net/