Расстояние от точки до прямой

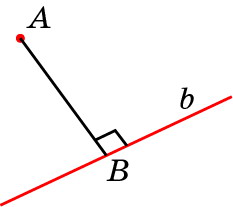
Расстояние от точки до прямой, не содержащей эту точку, есть длина отрезка перпендикуляра, проведённого из этой точки на прямую.

Здесь же целесообразно рассмотреть расстояние между параллельными прямыми - длина отрезка их общего перпендикуляра, то есть, расстояние от произвольной точки одной из переллельных прямых до другой.

Что используется:

• Метод площадей;
• Метод координат.    

Обучающая презентация* - скачать ...    

Задачи для самостоятельного решения**

1. В единичном куб АС₁ на диагоналях граней АD₁ и  D₁В₁ взяты точки Е и F так, что  D₁Е=1/3АD₁ ,D₁F=2/3D₁В₁. Найдите расстояние от точки D₁ до прямой EF.

2. В единичном кубе АС₁ найдите расстояние от точки В до прямой DА₁.

3. В единичном кубе найдите расстояние от  D₁ до PQ, если P – середина А₁В₁, Q – середина ВС.

4. В единичном кубе АС₁ найдите расстояние от А до BD₁.

5. В единичном кубе АС₁ найдите расстояние от точки D до прямой CА₁.

6. В единичном кубе ABCDA₁B₁C₁D₁ найти расстояние от точки D₁ до прямой PQ, где P и Q – середины соответственно ребер A₁B₁ и BC.

7.  В единичном кубе  AC₁ найдите расстояние от точки А до прямой  а)  B₁D₁; б)  A₁C; в) BD_1.

_8. В правильной треугольной призме АВСА₁В₁С₁, все рёбра которой равны 1, найдите расстояние от точки А до прямой ВС₁.

9. В правильной треугольной призме АВСА₁В₁С₁, высота равна 1, сторона основания равна 2. Найдите расстояние от точки А₁ до прямой ВС₁.

10. В правильной треугольной призме АВСА₁В₁С₁, высота равна 2, сторона основания равна 1. Найдите расстояние от точки В₁ до прямой АС₁.

11. Основание прямой призмы АВСDA₁B₁C₁D₁ - ромб АВСD, в котором АВ=10, АС=6√7. Боковое ребро АА₁ равно 3√21. Найдите расстояние от вершины В до прямой АС₁.

12. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁, все рёбра которой равны 1, найдите расстояние от точки А до прямой а) DE; б) D₁Е₁:  в) В₁С₁;  г ВЕ₁;  д) ВС₁;  е) СУ₁;  ж) СF₁;  з) СВ₁.

13. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁, стороны основания которой равны 5, а боковые рёбра равны 11, найдите расстояние от точки С до прямой А₁F₁.

14. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁, стороны основания которой равны 3, а боковые рёбра равны 2, найдите расстояние от точки Е до прямой В₁С₁.

15. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁, стороны основания которой равны 4, а боковые рёбра равны 3, найдите расстояние от точки С до прямой D₁E₁.

16. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁, все рёбра которой равны 1, найдите расстояние от точки А до прямой СВ₁.

17. В правильной шестиугольной призме AF₁, все рёбра которой равны 1, найдите расстояние от А до D₁F₁.

18. В правильной шестиугольной призме AF₁, все рёбра которой равны 1, найдите расстояние от А до ВС₁.

19. В правильной четырёхугольной пирамиде SABCD с основанием АВСD, сторона которого равна 2, а боковое ребро равно 4. Точка М - середина SD. Найдите расстояние от точки А до прямой МВ.

20. В правильной четырёхугольной пирамиде SABCD с основанием АВСD, сторона которого равна 1, а боковое ребро равно 0,5√3.  Найдите расстояние от точки С до прямой SA.

21. В тетраэдре DАВС, все рёбра которого равны 1, найти расстояние от точка А до прямой, проходящей через точку В и середину Е ребра СD.

22.  В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковое ребро - 2, найдите расстояние от С до прямой SА.

23.  В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковое ребро - 2, найдите расстояние от С до прямой SF.

24.  В правильной шестиугольной пирамиде МABCDEF, стороны основания которой равны 1, а боковое ребро - 2, найдите расстояние от F до прямой BT, где Т - середина ребра МС.  

25. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковое ребро - 2, найдите расстояние от F до BG, если G - середина SC.

* Презентация предоставлена  http://geometry2006.narod.ru/

** Задачи частично продоставлены http://alexlarin.net/