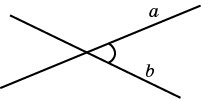
Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при пересечении прямых. Из определения логично следует, что 00< ∠ (a;b) 900.
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
Две прямые называются перпендикулярными, если угол между ними равен 900.
Угол между параллельными прямыми считается равным 00.
Методы решения:
- Классический: рассмотреть искомый угол как угол некоторого треугольника и нейти его используя теоремы планиметрии (теорема косинусов, теорема синусов, обратная теорема Пифагора, метод площадей и др.).
- Векторно-координатный метод: возможно использование следующих формул
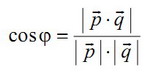 или
или 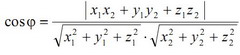 , где
, где 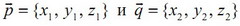 - координаты направляющих векторов.
- координаты направляющих векторов.
Обучающая презентация* - скачать... и ещё одна презентация* скачать... 
Задачи для самостоятельного решения**
1. В кубе АС1 найдите угол между прямыми А1D и D1Е, где Е - середина стороны СС1.
2. В кубе АС1 найдите угол между прямыми EF и PQ, где E, F, P и Q - середины рёбер DD1, АА1, В1С1 соответственно.
3. В кубе АС1 найдите угол между прямыми AD1 и DM, где М - середина ребра D1С1.
4. В кубе АС1 найдите угол между прямыми ВD1 и АЕ, где Е - середина ребра А1В1.
5. Точка Е - середина ребра DD1 куба АС1. Найдите угол между прямыми СЕ и АС1.
6. На ребре СС1 куба АС1 отмечена точка Е так, что СЕ:ЕС1=1:2. Найдите угол между прямыми ВЕ и АС1.
7. В единичном кубе АС1 найти угол между прямыми АЕ и DF, где Е и F - точки, расположенные на рёбрах CD и С1D1 так, что DE=1|3CD, С1F=1/3C1D1.
8. В кубе АС1 E и F - середины рёбер А1В1 и В1С1 соответственно. Найдите косинус угла между прямыми АЕ и BF.
9. В кубе АС1 E и F - середины рёбер А1В1 и D1С1 соответственно. Найдите косинус угла между прямыми АЕ и BF.
10. В кубе АС1 к диагонали А1С провели перпендикуляры из вершин А и В. Найдите угол между этими перпендикулярами.
11. К диагонали куба провели перпендикуляры из остальных вершин куба. На сколько частей и в каком отношении основания этих перпендикуляров разделили эту диагональ?
12. В кубе АС1 к диагонали А1С провели перпендикуляры из середин рёбер АВ и AD. Найдите угол между этими перпендикулярами.
13. Дан прямоугольный параллелепипед АС1. Его диагональ В1D составляет с ребром АD угол в 450, а с ребром DС угол в 600. Найдите угол между прямыми В1D и DD1.
14. Непересекающиеся диагонали двух смежных боковых граней прямоугольного параллелепипеда образуют с плоскостью его основания углы
α
и ß. Найдите угол между этими диагоналями.
15. В правильной треугольной призме АВСА1В1С1, все рёбра которой равны 1, найдите угол между прямыми АС1 и В1С.
16. В правильной треугольной призме АВСА1В1С1, все рёбра которой равны 1, найдите косинус угла между прямыми а) АВ и СА1; б) АВ1 и С1В.
17. Сторона основания правильной треугольной призме АВСА1В1С1 равна 8. Высота этой призмы равна 6. Найдите угол между прямыми СА1 и АВ1.
18. В правильной треугольной призме АВСА1В1С1, все рёбра которой равны 1, точка D - середина ребра А1В1. Найдите косинус угла между прямыми АD и ВС1.
19. В правильной треугольной призме АВСА1В1С1, все рёбра которой равны 1, точки D, Е - серединв рёбер А1В1 и В1С1 соответственно. Найдите косинус угла между прямыми АD и ВЕ.
20. В основании прямой призмы АВСА1В1С1 лежит равнобедренный прямоугольный треугольник АВС с гипотенузой АВ, равной 8√2. Высота этой призмы равна 6. Найдите угол между прямыми АС1 и СВ1.
21. В правильной четырёхугольной призме АВСDA1B1C1D1 сторона основания равна 12, а боковое ребро - 5. Найдите угол между прямыми АС и ВС1.
22. В правильной шестиугольной призме АВСDEFA1B1C1D1E1F1, все рёбра которой равны 1, найдите угол между прямыми АВ1 и F1B.
23. В правильной шестиугольной призме АВСDEFA1B1C1D1E1F1, все рёбра которой равны 1, найдите угол между прямыми АВ1 и С1B.
24. В правильной шестиугольной призме АВСDEFA1B1C1D1E1F1, все рёбра которой равны 1, найдите косинус угла между прямыми АВ1 и D1B.
25. В правильной шестиугольной призме АВСDEFA1B1C1D1E1F1, все рёбра которой равны 1, точка G - середина ребра А1В1. Найдите
косинус угла между прямыми АG и С1B.
26. В правильной шестиугольной призме АВСDEFA1B1C1D1E1F1, все рёбра которой равны 1, точка G - середина ребра А1В1. Найдите
косинус угла между прямыми АG и D1B.
27. В правильной шестиугольной призме АВСDEFA1B1C1D1E1F1, все рёбра которой равны 1, точки G и Н - середины рёбер А1В1 и В1С1. Найдите косинус угла между прямыми АG и НB.
28. Найдите угол между непересекающимися медианами граней правильного тетраэдра.
29. В правильной тетраэдре АВСD точка К - середина ВD, точка М - середина ВС. Найдите угол между прямыми АК и DМ.
30. В тетраэдре АВСD известно, что АС=ВD=14, ВС=АD=13, АВ=СD=15. Найдите угол между прямыми АС и ВD.
31. Рёбра АD и ВС пирамиды DАВС равны 24 и 10. Расстояние между серединами рёбер ВD и АС равно 13. Найдите угол между прямыми АD и ВС.
32. В правильной четырёхугольной пирамиде SАВСD (с вершиной S) боковое ребро равно стороне основания. Точка М - середина ребра SВ. Найдите угол между прямыми СМ и SО, где точка О - центр основания пирамиды.
33. В правильной четырёхугольной пирамиде SАВСD (с вершиной S), все рёбра которой равны 1, точки Е и F - середины рёбер SВ и SС соответственно. Найдите косинус угла между прямыми АЕ и ВF.
34. Угол между боковыми рёбрами правильной четырёхугольной пирамиды, не лежащими в одной грани, равен 1200. Найдите плоский угол при вершине пирамиды.
35. В правильной шестиугольной пирамиде МАВСDEF, стороны основания которой равны 1, а боковые рёбра равны 2, найти косинус угла между МВ и АD.
36. В правильной шестиугольной пирамиде МАВСDEF, стороны основания которой равны 1, а боковые рёбра равны 2, точка К - середина ребра МD. Найти косинус угла между МА и FK.
37. В правильной шестиугольной пирамиде SАВСDEF, стороны основания которой равны 1, а боковые рёбра равны 2, найти косинус угла между SВ и АE.
38. В правильной шестиугольной пирамиде SАВСDEF, стороны основания которой равны 1, а боковые рёбра равны 2, найти косинус угла между SВ и АD.
39. В правильной шестиугольной пирамиде SАВСDEF, основанием АВСDEF сторона основания равна 2, а боковые рёбра равны 4. Точка М - середина SE. Найти угол между прямыми SB и CM.
* Презентация предоставлена http://geometry2006.narod.ru/
** Задачи частично продоставлены http://alexlarin.net/