Расстояние между двумя точками А и В в пространстве можно вычислить

1) как длину отрезка АВ, если отрезок АВ удастся включить в некоторый треугольник в качестве одной из его сторон или отрезка, связанного с треугольником (медиана, высота, биссектриса);

2) по формуле  

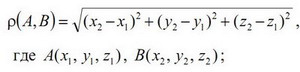
3) по формуле

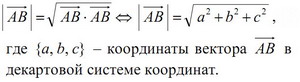
Что используется:

• Теорема синусов;

• Теорема косинусов;
• Метод площадей;
• Координатный метод.

Обучающая презентация* - скачать...   

Задачи для самостоятельного решения**

1.      В единичном кубе АС₁ на диагоналях граней АD₁ и  D₁В₁ взяты точки Е и F так, что  D₁Е=1/3АD₁ ,D₁F=2/3D₁В₁. Найдите длину отрезка ЕF.

2.      В единичном кубе АС₁ точки Е и К – середины рёбер АА₁ и СD соответственно, а точка М расположена на диагонали В₁D₁ так, что В₁М=2МD₁. Найдите расстояние между точками Q и L, где Q – середина отрезка ЕМ, а L – точка отрезка ЕМ такая, что МL=2LК.

3.    Рёбра правильной четырёхугольной призмы равны 1, 4, 4. Найдите расстояние от вершины до центра основания призмы, не содержащего эту вершину.

4.     В единичном кубе АС₁ точки Е, К и L – середины рёбер АА₁, СD и В₁С₁  соответственно, а точки М и N расположены соответственно на отрезках ЕК и LК так, что ЕМ:МК=2:№, а LN:NK=1:4. Найдите длину отрезка MN.

5.     В правильной треугольной призме АВСА₁В₁С₁ на рёбрах АВ и  В₁С₁ выбраны точки Е и К так, что АЕ:ЕВ=1:2, а В₁К: КС₁=5:1. Найдите длину отрезка ЕК, если сторона основания призмы равна 6, а боковое ребро равно 2.

6.    В правильной шестиугольной призме  АВСDEFА₁В₁С₁D₁E₁F₁,все рёбра которой равны 2, найдите расстояние от точки А до точек а) С₁; б) D₁; в) M, если М - центр грани DD₁EE₁.  

7.     В правильной шестиугольной призме  АВСDEFА₁В₁С₁D₁E₁F₁,все рёбра которой равны 1, найдите расстояние между точками А и E₁.  

8.     В правильной четырёхугольной пиримиде SABCD, сторона основания и боковое ребро которой равны 4√2  и 5 соответственно. Найдите растояние между точами Е и К, если известно, что Е лежит на боковом ребре SВ и SЕ=2ВЕ, а К - на стороне основания АD и АК=3КD.

* Презентация предоставлена  http://geometry2006.narod.ru/

** Задачи частично продоставлены http://alexlarin.net/