| Главная » Статьи » Мои статьи |
Прежде чем решать задачи на касательную к окружности, полезно вспомнить некоторые факты:
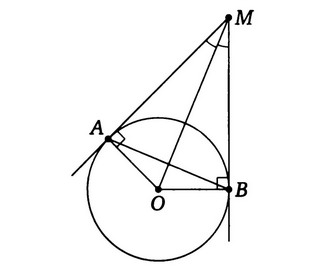
1. Пусть из точки М к окружности проведена касательная МА (А - точка касания). Тогда радиус, проведённый в точку касания, перпендикулярен касательной (АО перпендикулярен АМ). 2. Если из точки М проведены две касательные МА и ВМ (А, В - точки касания), то отрезки касательных, проведённых из одной точки равны (АМ=ВМ), равны углы АМО и ВМО (О - центр окружности), отрезок АВ перпендикулярен ОМ. Задания для урока: 1. В треугольнике АВС угол А равен 1200. Окружность радиуса r касается стороны ВС и продолжений сторон АС и АВ. Найдите периметр треугольника АВС. 2. На окружности радиуса r выбраны три точки таким образом, что окружность оказалась разделённой на три дуги таким образом, что градусные меры их относятся как 3:4:5. В точках деления к окружностям проведены касательные. Найдите площадь треугольника, образованного этими касательными. 3. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 5 и 12. Найдите катеты треугольника. 4. Радиусы двух окружностей равны 27 и 13, а расстояние между их центрами - 50. Найдите длины общих касательных к этим окружностям. Задания для самостоятельного решения: 1. Две прямые, проходящие через точку М, лежащую вне окружности с центром О, касаются окружности в точках А и В.Отрезок АМ делится окружностью пополам. В каком отношении отрезок ОМ делится прямой АВ? 2. В окружности радиусом R=4 проведены хорда АВ и диаметр АК, образующий с хордой угол π/8. В точке В проведена касательная к окружности, пересекающая продолжение диаметра АК в точке С. Найдите медиану АМ треугольника АВС. 3. Две окружности радиусов 4 и 3 с центрами в точках О1 и О2 касаются некоторой прямой в точках М1 и М2 соответственоо и лежат по разные стороны от этой прямой. Отношение отрезков О1О2 и М1М2 равно 2/ √ 3 . Найдите О1О2 . | |
| Просмотров: 3067 | |
| Всего комментариев: 0 | |