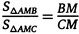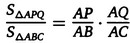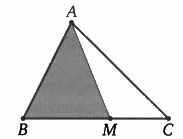
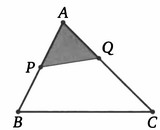
Для успешного решения задач, связанных с нахождением площадей плоских фигур, необходимо знать некоторую теорию:

1) 5 формул площади треугольника;

2) Медиана делит треугольник на два равновеликих;

3) Три медианы одного треугольника, пересекаясь в одной точке делят треугольник на 6 равновеликих;

4) Отношение площадей подобных треугольников равно квадрату коэффициента подобия;

5) Если точка M лежит на стороне BC треугольника ABC, то площади треугольников АМB и АМС пропорциональны отрезкам ВМ и СМ (не сложно доказать , используя формулу площади треугольника через высоту)

6) Если прямая пересекает стороны АВ и АС треугольника АВС (или их продолжения) в точках Р и Q соответственно, то выполняется следующее соотношение (тоже не сложно доказать, используя формулу площади треугольника с синусом)

Задачи для урока:

1) Площадь треугольника равна 4. Найдите площадь треугольника, сторонами которого являются отрезки, соединяющие середины сторон данного треугольника.

2) Найдите площадь треугольника АВС, если АС=3, ВС=4, а медианы, проведённые из вершин А и В, перпендикулярны (ЕГЭ-2011).

3) Диагонали АС и ВD трапеции АВСD пересекаются в точке Е. Найдите площадь трапеции, если S(АЕD)=9, а точка Е делит одну из диагоналей в отношении 1:3 (ЕГЭ-2011)

Задания для самостоятельной работы:

1) Сторона треугольника равна 36. прямая, параллельная этой стороне, делит площадь треугольника пополам. Найдите длину отрезка этой прямой,заключённого между сторонами треугольника.

2) Боковая сторона АВ трапеции АВСD равна m, а расстояние от середины СD до прямой АВ равно n. Найдите площадь трапеции.